We are getting closer to understanding the physics of curling

Last year, 2024, marked the 100th anniversary of the first scientific article that I’m aware of that investigated the physics behind the sport of curling; a 1924 paper [5] by E. L. Harrington and his colleagues in the College of Engineering of the University of Saskatchewan in Saskatoon.

In the 100 years since Harrington’s work, scientists and engineers have investigated various aspects of the sport, but our understanding of one of the sport’s singular fundamentals – why does a curling stone “curl” – remains incomplete, if not vague. There have been dozens of articles, authored by scientists and engineers from Canada, Sweden, Finland, China, Japan, and Korea, that have investigated the question of why stones curl the way they do, frequently contradicting each other’s mathematical models and none of them fully explaining all of a stone’s observed behaviours. At the same time, there are other aspects of the sport, particularly surrounding brushing, that have not been studied extensively and remain puzzling, at least in a scientific context, even though some of the behaviours are well-understood by experienced players.

Here are a few of these research topics, in no particular order; and by no means is this a complete list:

It is well known that once a stone traverses a path several times, the ice becomes “keener” down that path; but if the ice is allowed to “rest”, then the ice reverts to a slower speed. How precisely does this occur?
Why does the coefficient of friction of the ice surface with a curling stone vary, depending on the stone’s velocity? In other words, why is the deceleration of a curling stone approximately logarithmic, rather than linear? (see Figure below).
It is known that the lowest coefficient of friction for ice occurs at a temperature of -7C, which is the ice temperature used in other sports, such as speed skating. So what is it about curling ice that makes the usual surface temperature three degrees warmer, at -4C?
In a national or provincial championship played on arena ice, what exactly happens at the 5th end break when the ice is mopped, so that the sheet is keener at the start of the 6th end?
Why does brushing down a path result in keener ice for subsequent stones down the same path? And even if subsequent stones are not brushed?
Why does accentuating curl (“carving”) not work all the time? (Aside: it doesn’t – sometimes the stone goes straighter regardless of the brushing motion, and is dependent on “ice conditions”. )
Several teams on the Tour now confirm that “knifing” (turning the orientation of the brush head 90 degrees when brushing) slows down a stone. How does this occur?
Why do some brush heads “work” better than others, even though all brush heads in competitive play are required to use the identical World Curling-approved, mustard-yellow, 520D nylon fabric?
What are precisely the mechanics surrounding the delivery of stones with lots of rotation? (sometimes termed a “spinner”; see video clip below from John Cullen).
Is there a force threshold that must be met to induce particular behaviours when brushing a stone? Is there a limit, that is, a situation where additional force yields no greater effect?

There are lots of others.

A reasonable question to ask is if any of these details actually matter at the end of the day. We perform all kinds of tasks without understanding the physics behind them. Children don’t have to understand the physics or mechanics of riding a bicycle; they just do it. Similarly, motorcyclists don’t have to understand the physics of why a smaller front wheel on a motorcycle results in more responsive handling, or why “pushing” on a handlebar steers the bike in that direction once the motorcycle attains a certain velocity. And so it is for curling athletes: they only need to know that if they do X, then they will produce behaviour Y in the trajectory of a curling stone. The underlying theories don’t really matter that much, and the vast majority of players aren’t engineers.

However, understanding these phenomena do matter, in a myriad of ways. One is to provide the scientific basis for regulating curling equipment, particularly brushes. Another is to help determine what the rules of the sport should permit, and what the rules should disallow. A third is to provide better science to assist ice technicians in making and maintaining better surfaces on which to play.

With respect to brushing, for example, my colleague John Newhook and I have been careful to describe brushing with respect to “interaction forces” between a stone and the ice, and between the brush and the ice. It is true that curling is described as the sport that is “all about friction” but the problem is that the details of those stone-ice interactions remain not well understood. Fortunately, modern, sophisticated technology is helping to uncover the significant complexities within the sport of curling, and some recently-published work has me quite excited about the next few years of research. As one example, in a super-interesting paper [6] Takao Kameda and his team at the Kitami Institute of Technology described the use of a probe-type surface roughness meter (SJ-210, Mitutoyo Corporation, Japan) to measure the roughness of a stone’s running band to ensure consistent results in their testing of stone trajectories.

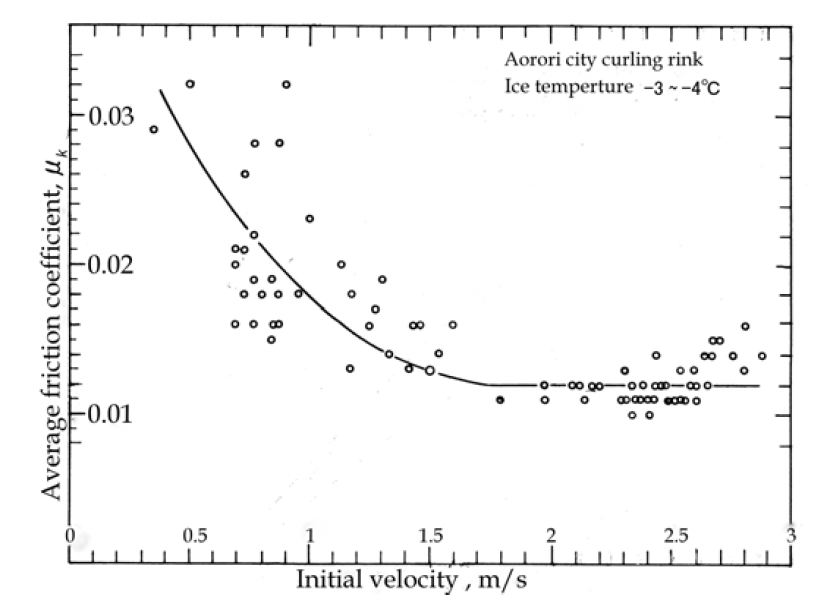
Coefficient of friction (CoF) of ice to a curling stone, from Tusima [15]. A stone velocity of approximately 2.1 m/sec is “draw weight” on decent ice. Note how the coefficient increases as the stone slows.

Example of a stone thrown with considerably greater rotation than what is commonly seen during play. Commentary by John Cullen.

The physics are really complicated

Ice is a complex material whose properties change significantly by temperature, especially when the temperature is near the freezing point [3,4,7,8,12,13,15]. Ice is both brittle and slippery, at least at higher temperatures near freezing; it is also subject to wear, and is easily scratched by harder surfaces like granite. Ice can be warmed through both pressure and friction [7], though it appears that in a curling context the pressures delivered to the ice through the stone itself, or a brush head, are insufficient; it is the friction force delivered by stones and brushes that are at play in curling. The surface properties of ice are also influenced by the ambient air temperature, relative humidity, dew point, existence of frost, water impurities, and potentially other factors.

Recent studies of ice in other sport contexts, largely speed skating, have discovered that the surface of ice has a “quasi-liquid layer” [4,13,16] of a very small depth (measured in nanometers). Recent work has shown that the surface of ice is comprised of two different types of water molecules that have differing numbers of hydrogen bonds. These molecules constantly “roll over” one another in response to frictional forces. However, the properties of this quasi-liquid layer remain largely unknown, and the influence of this quasi-liquid layer in curling is also largely unknown.

In other words, ice is a very difficult substance to model, and to assess empirically.

Some (really) interesting recent work

Despite the complexities of ice, a few articles published in the last year are exciting in that they have the potential to further our understanding of the physics of curling in a significant way.

One of these is the article at right [2] by Alex Brown, a now-retired professor at Polytechnique Montrèal (click on the image to view the article’s first two pages). In detail, Brown outlines his reasoning that the friction from curling stones follows the Stribeck curve, a well-known phenomenon in Tribology (the study of friction).

Brown proposes that curling stones go through three distinct phases of friction during their trajectory:

Wet friction at high speeds, due to lubrication from a thin film of water;
A mixed hydrodynamic and abrasive friction at moderate speeds, beginning at the break point, where the running band begins to cause striations in pebble, “biting” into the ice;
A dry friction phase at the end of the stone’s travel where no water lubrication exists.

Used with permission of Canadian Journal of Physics, from “Correlations between curling stone frictions and tribology’s Stribeck curve: concepts to consider”, Alex C. Brown, Volume 102(12), December 2024; permission conveyed through Copyright Clearance Center, Inc.

In most circumstances, curlers understand the occurrence and origins of particular behaviors of rocks on ice, such as an early easy glide characterized by a mild deceleration, followed by a break into a decidedly more severe, ever-increasing deceleration. With concepts borrowed from the Stribeck curve, this contribution suggests important new perspectives on deliveries to the button.

Brown [2], pp. 641

Brown argues that stones travelling at high speeds – greater than 0.6 m/sec – benefit from very low coefficients of friction (near 0.01) resulting alone from shearing-stress friction within that lubricating water film, and the CoF increases very slowly until the transition to the second phase: which we commonly call the “break point”, when mixed-mode frictional effects take over.

The really interesting thing is where does the lubricating water come from, since the ice temperature is nominally at -4C. Interestingly, quite recently Sean Maw and his research team at the University of Saskatchewan have shown that curling stones actually cause pebble to warm as the stone travels over it, and proved it using a highly sensitive infrared camera. Brown’s ideas confirm Nyberg’s [11] findings that there was no evidence of striations in pebble when stones were moving at higher velocities; essentially, the stones were hydroplaning.

This is really interesting work that unifies a number of theories and empirical measurements from other researchers, and these ideas could provide a framework for further research into the physics of curling. Moreover, there are obvious implications for the application of brushing during the three phases.

Another article by Ziegler [18], still unpublished, also discusses the modeling of a stone’s behaviour to the Stribeck curve and also offers a model of behaviour for “spinner” shots that have much more rotation than is usual.

These works provide a potential framework for a more complete understanding of the physics of curling, and give us clues as to what empirical experiments can be performed to prove or disprove these new models. I expect some very interesting research on this topic in the new future.

Pebble abrasion from curling stones

Players well realize that pebble wears throughout a game as stones are thrown. At right, a recent article by Yanagi et al. [17] documents the wear of pebble after the passing of stones, and how as pebble height is lost the contact area with the running band increases.

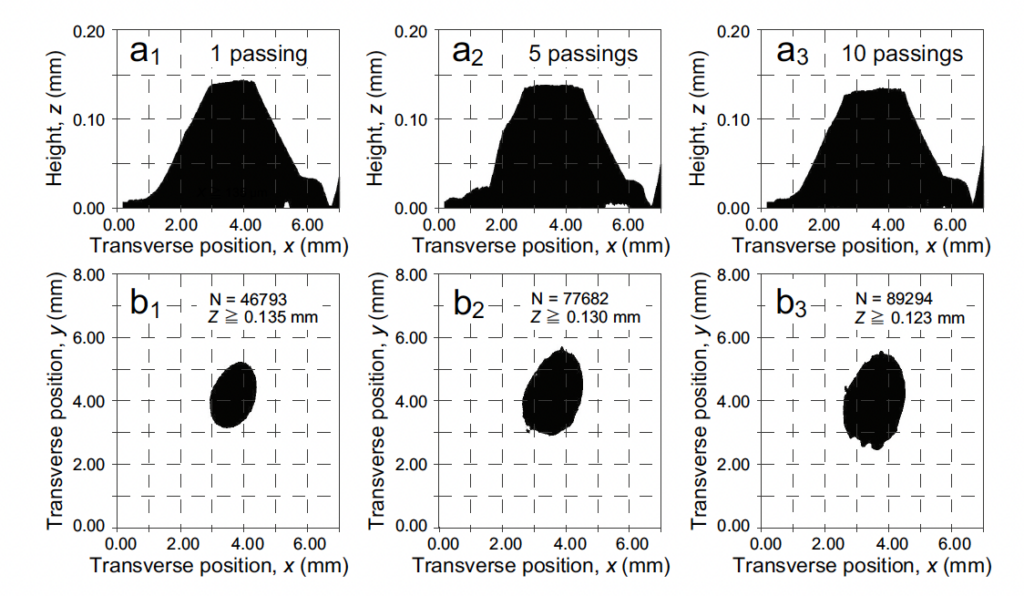
In addition, the abrasion caused by a stone’s running band creates striations across the pebble, and these can be seen with enlarged macro digital photography. The photographs below show two images of the same pebble, before and after a stone passes over it.

The photographs below are courtesy of Sean Maw and the University of Saskatchewan. Photo credits: Makayla Robinson, Derek Elvin, Eugene Hritzuk, and Sean Maw and his research team at the University of Saskatchewan.

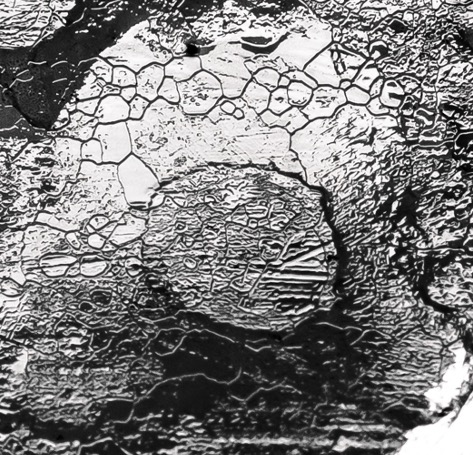
Base pebble image.

Pebble after being brushed, followed by a stone. Evidence of the brushing can be seen in the minor striations going from bottom right to top left, whereas the much deeper striations from the running band at the top of the pebble go from left to right.

Pebble abrasion from brushing

Brushing creates at least two effects on pebble: a heating effect, which is well known [1,9] and a mechanical effect that results in abrasion, which has been largely ignored to date. The amount of abrasion depends on a variety of factors, including the duration of the brushing and the force profile of the athlete, to name but two.

In their experiments, Sean Maw and his team evaluated pebble abrasion from brushing over three related effects: polishing, texture, and erasure. All of the tests were conducted using a Hardline IcePad brush with World Curling-approved competitive fabric. In each case, five brushing half-strokes (push forward, pull backward, forward, backward, forward) were performed to simulate a single brusher and their brushing effects as the stone slows near the house on a draw shot. Erasure was measured on a four-point qualitative scale, ranging from minor smoothing to the complete elimination of the nipped pebble surface.

This experimental regimen permits us to now experiment with different brushes and different brushing techniques (knifing in particular) to assess their abrasion to pebble in addition to their impact on a stone’s trajectory to better understand the physics behind brushing.

The photographs are courtesy of Sean Maw and the University of Saskatchewan. Photo credits: Grant McEwen Harris, Kelly Salmon, Derek Elvin, Eugene Hritzuk, and Sean Maw and his research team at the University of Saskatchewan.

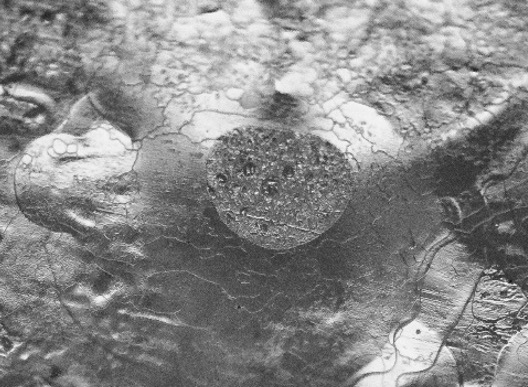
Base pebble image for Level 1 erasure.

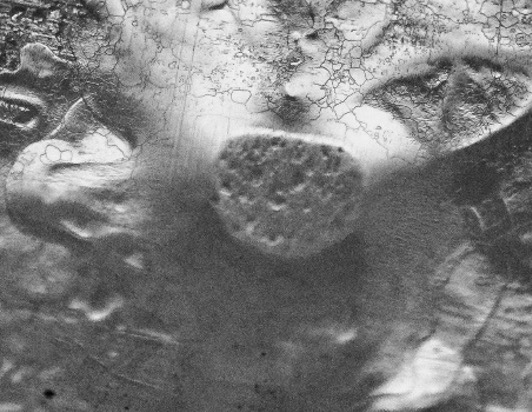
Level 1 pebble erasure. Minor smoothing of the pebble edge and/or surface but the nipped portion remains clearly visible.

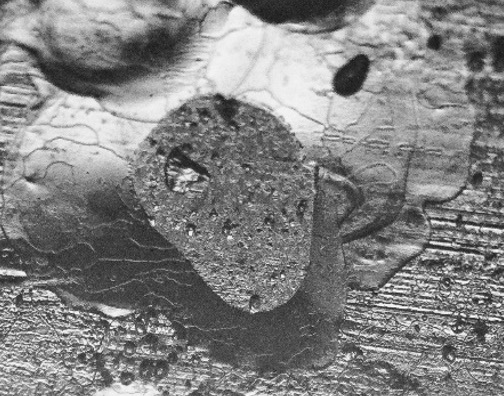
Base pebble image for Level 2 erasure. The scratches left behind by the scraping blade on the surface of the ice sheet prior to pebbling, roughly from left-to-right across the image, are clearly visible here.

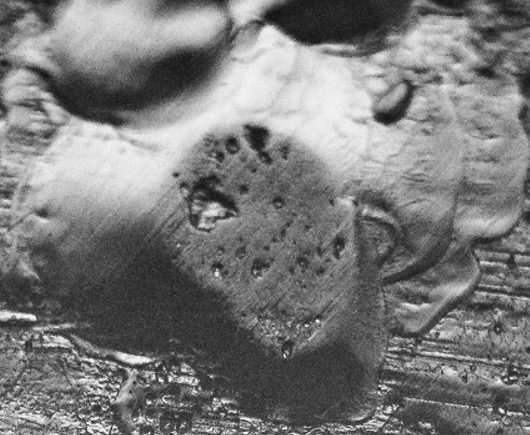
Level 2 pebble erasure. The pebble retains a defined edge, but is much smoother than the nipped pebble at left. Note the faint striations left behind by the smoothing action of the brushing fabric, from bottom left to top right.

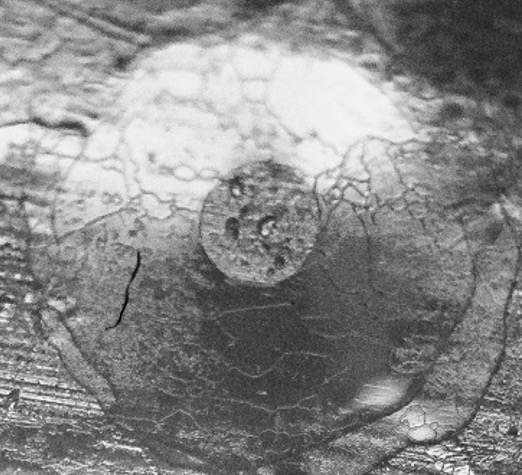
Base pebble image for Level 3 erasure.

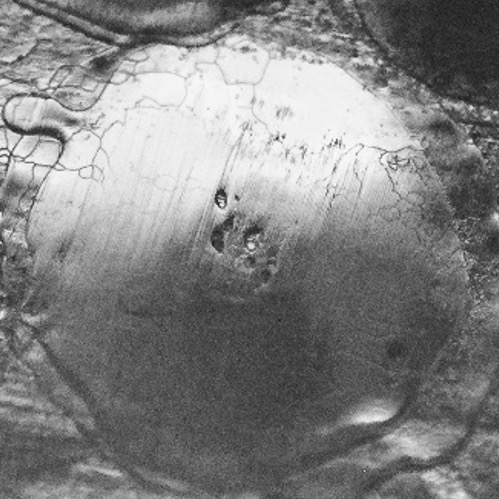
Level 3 pebble erasure. The edge of the nipped portion of the top of the pebble is no longer present, though some detail in the top of the pebble remains.

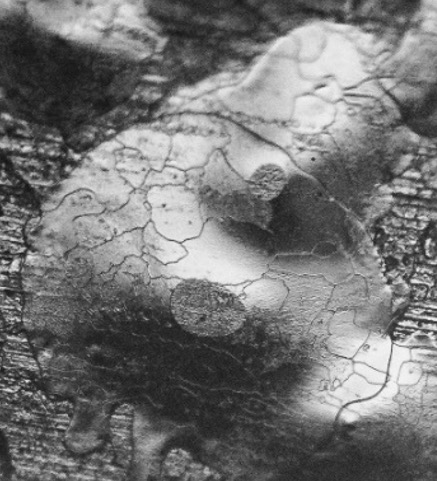
Base image for Level 4 erasure.

Level 4 pebble erasure. While the pebble itself is still present, the nipped portion is now eradicated.

Summary

Significant progress has been made in the understanding of the physics of curling in just the past ten years, aided by technology improvements in measurement systems and digital photography. But there remains a lot of work to do before we are, for example, able to regulate brushing equipment to meet the needs of the sport, and of the equipment manufacturers who produce these products. Nonetheless I am encouraged by this research and remain hopeful that we can build on these results in the very near term.

References

If possible, I’ve included links to the articles below. Many, but not all, are publicly available through a Creative Commons license and viewable/downloadable for free.

[1] Bradley, J. L. (December 2009). The sports science of curling: a practical review. Journal of Sports Science and Medicine 8(4), pp 495-500. Available at https://pubmed.ncbi.nlm.nih.gov/24149588/

[2] Brown, Alex C. (December 2024). Correlations between curling stone frictions and tribology’s Stribeck curve: concepts to consider. Canadian Journal of Physics 102(12), pp. 633-645. DOI: https://doi.org/10.1139/cjp-2024-0095.

[3] Calderon, C.T. and Mohazzabi, P. (2018) Premelting, Pressure Melting, and Regelation of Ice Revisited. Journal of Applied Mathematics and Physics 6, pp. 2181-2191. DOI: https://dx.doi.org/10.4236/jamp.2018.611183.

[4] Canale, L, Comtet, J., Niguès, A, et al. (November 2019). Nanorheology of Interfacial Water during Ice Gliding. Physical Review X 9, 9 pages. DOI: https://doi.org/10.1103/PhysRevX.9.041025.

[5] Harrington, E. L. (1924). An experimental study of the motion of curling stones. Transactions and Proceedings of the Royal Society of Canada 8, pp. 247-259.

[6] Kameda, T. Shikano, D., Harada, S, Yanagi, S, and Sado, K. (2020). The importance of the surface roughness and running band area on the bottom of a stone for the curling phenomenon. Scientific Reports 10(11), 9 pages. DOI: https://doi.org/10.1038/s41598-020-76660-8

[7] Liefferink, R. W., Hsia, F.-C., Weber, B., and Bonn, D. (February 2021). Friction on Ice: How Temperature, Pressure, and Speed Control the Slipperiness of Ice. Physical Review X 11, 13 pages. DOI: https://doi.org/10.1103/PhysRevX.11.011025.

[8] Makkonen, L. and Tianmäki, M. (March 2014). Modeling the friction of ice. Cold Regions Science and Technology 102, pp. 84-93. DOI: http://dx.doi.org/10.1016/j.coldregions.2014.03.002.

[9] Marmo, B., Farrow, I. S., Buckingham, M.-P., and Blackford, J. R. (October 2006). Frictional heat generated by sweeping in curling and its effect on ice friction. Proceedings of the Institution of Mechanical Engineers Part L, Journal of Materials Design and Applications 220(4), pp. 189-197. DOI: http://dx.doi.org/10.1243/14644207JMDA93

[10] Murata, J. (September 2022). Study of curling mechanism by precision kinematic measurements of curling stone’s motion. Scientific Reports 12, 8 pages. DOI: https://doi.org/10.1038/s41598-022-19303-4

[11] Nyberg H., Alfredsson S., Hogmark S., Jacobson S., The asymmetrical friction mechanism that puts the curl in the curling stone. Wear 301, pp. 583-589, 2013. DOI: https://doi.org/10.1016/j.wear.2013.01.051.

[12] Persson, B. N. J. (December 2015). Ice Friction: Role of non-uniform frictional heating and ice premelting. Journal of Chemical Physics 143, 9 pages. DOI: https://doi.org/10.1063/1.4936299.

[13] Sazaki, G., Zeipeda, S., Nakatsubo, Y. and Furukawa, Y. (January 2012). Quasi-liquid layers on ice crystal surfaces are made up of two different phases. Proceedings of the National Academy of Sciences 109(4), pp. 1052-1055. DOI: https://doi.org/10.1073/pnas.1116685109.

[14] Sonobe, H., Aoki, Y, Miya, O. et al. (September 2024). Sweeping effect on curling and friction estimation. Sports Engineering 27(31), 11 pages. DOI: https://doi.org/10.1007/s12283-024-00473-5

[15] Tusima, K. (April 2011). Adhesion Theory for Low Friction on Ice. In Chrib T., editor, New Tribological Ways, InTech, pp. 301-328. DOI: https://doi.org/10.5772/15085.

[16] Weber, B., Nagata, Y., Ketzetzi S. et al. (June 2018). Molecular Insight into the Slipperiness of Ice. Journal of Physical Chemistry Letters 9(11), pp. 2838-2842. DOI: http://dx.doi.org/10.1021/acs.jpclett.8b01188.

[17] Yanagi, S., Kameda, T., Harada, Y, and Sado K. (May 2024). Characteristics of pebble shape and the amount of pebble abrasion measured with a replica reproduced on a curling rink. Scientific Reports 14(11463). DOI: https://doi.org/10.1038/s41598-024-62247-0.

[18] Ziegler, M. (February 2024). The Split Friction Model – The Isotropic Origin of the Lateral Force in Curling. Unpublished manuscript. DOI: https://doi.org/10.21203/rs.3.rs-367477/v3.